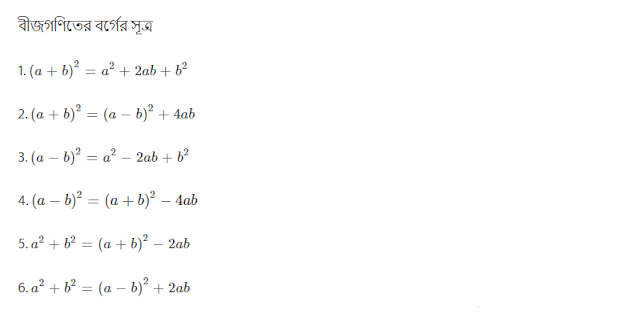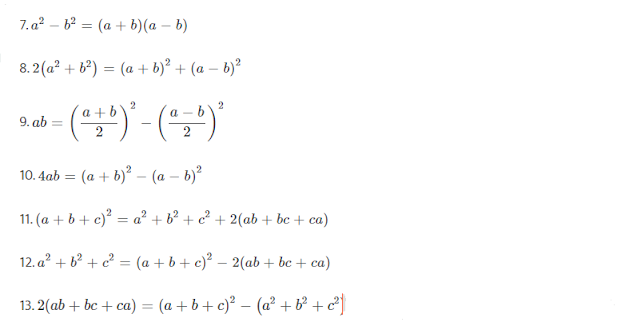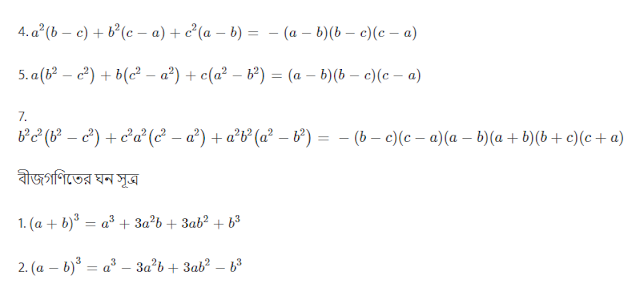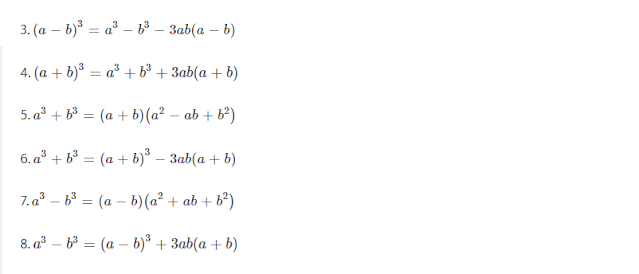বীজগণিতের সূত্র সমূহ
এর আগে আমার প্রয়োজনীয় বীজগণিতের সূত্র সমূহ নিয়ে আলোচনা করেছি । ঔ আর্টিকেলে শুধু মাত্র Algebra - এর অংক করার সূত্র দেওয়া হয়েছে । আজকের আর্টকেলের আমরা যে সকল বীজগণিতের সূত্র সমূহ উল্লেখ করেছি । যেগুলোর মাধ্যমে বীজগণিতিক রাশি , সূচক ও লগারিদম , সসীম ধারা সহ সকল বীজগণিত অংক করা যাবে । আজকের আর্টিকেলে বর্ণিত বীজগণিতের সূত্রাবলী - র মাধ্যমে যে কোনো বীজগণিত অংক করা যাবে । শুধু তাই নয় এ সকল বীজগণিতের সূত্র সমূহ যে কোনো প্রতিযোগীতা মূলক পরীক্ষার জন্য খুবই গুরুত্বপূর্ণ । বীজগণিতের সূত্রাবলী প্রয়োগ করে যে কোনো অংক সহজেই সামাধান করা যায় । এছাড়াও বাস্তব জীবনের বিভিন্ন গাণিতিক সমস্যায় বীজগণিতের সূত্র সমূহ - এর প্রয়োগ রয়েছে ।
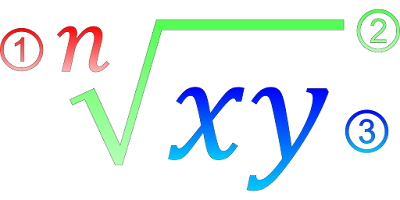 |
| বীজগণিতের সূত্র সমূহ |
পাটিগণিত ও জ্যামিতি -র মাধ্যমে যে সমস্যার সমাধান দুঃসাধ্য বীজগণিতের সূত্র সমূহ ব্যবহার করে তা অনেক সহজ হয়ে যায় । তাই সকল শিক্ষার্থীদের বীজগণিতের সূত্রাবলী জানা অনেক গুরুত্বপূর্ণ ।
বীজগণিতীয় প্রতীক দ্বারা প্রকাশিত যেকোন সাধারণ নিয়ম বা সিদ্ধান্তকে বীজগণিতীয় সূত্র বলে । - বীজগণিতের সূত্র সমূহ
আর্টিকেল শেষে জানতে পারবেন
আরো পড়তে পারেন
মানুষ মৃত অবস্থা থেকে জেগে ওঠে কেন !
নবম - দশম শ্রেণির গণিত সৃজনশীল প্রশ্ন
বীজগণিতের বর্গের সূত্র
1. `\left(a+b\right)^2=a^2+2ab+b^2`
2. `\left(a+b\right)^2=(a-b)^2+4ab`
3. `\left(a-b\right)^2=a^2-2ab+b^2`
4. `\left(a-b\right)^2=(a+b)^2-4ab`
5. `a^2+b^2=(a+b)^2-2ab`
6. `a^2+b^2=(a-b)^2+2ab`
7. `a^2-b^2=(a+b)(a-b)`
8. `2(a^2+b^2)=(a+b)^2+(a-b)^2`
9. `ab=\left(\frac{a+b}2\right)^2-\left(\frac{a-b}2\right)^2`
10. `4ab=\left(a+b\right)^2-\left(a-b\right)^2`
11. `\left(a+b+c\right)^2=a^2+b^2+c^2+2(ab+bc+ca)`
12. `a^2+b^2+c^2=(a+b+c)^2-2(ab+bc+ca)`
13. `2\left(ab+bc+ca\right)=\left(a+b+c\right)^2-(a^2+b^2+c^2)`
14. `\left(a-b-c\right)^2=a^2+b^2+c^2-\left(ab+bc+ca\right)`
15. `(x+a)(x+b)=x^2+(a+b)x+ab`
16. `(x+a)(x-b)=x^2+(a-b)x-ab`
17. `(x-a)(x+b)=x^2-(a-b)x-ab`
18. `(x-a)(x-b)=x^2-(a+b)x+ab`
19. `(p+x)(q+x)=pq+(p+q)x+x^2`
20. `(p+x)(q+x)(r+x)=pqr+(pq+qr+rp)x+(p+q+r)x^2+x^3`
21. `(x+a)(x+b)(x+c)=x^3+(a+b+c)x^2+(ab+bc+ca)x+abc`
বীজগণিতের চক্র ক্রমিক সূত্র
1. `(a+b)(b+c)(c+a)+abc=(a+b+c)(ab+bc+ca)`
2.` (ab+bc+ca)(a+b+c)-abc=(a+b)(b+c)(c+a)`
3. `bc(b-c)+ca(c-a)+ab(a-b)=-(b-c)(c-a)(a-b)`
4. `a^2(b-c)+b^2(c-a)+c^2(a-b)=-(a-b)(b-c)(c-a)`
5. `a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)=(a-b)(b-c)(c-a)`
7. `b^2c^2(b^2-c^2)+c^2a^2(c^2-a^2)+a^2b^2(a^2-b^2)=-(b-c)(c-a)(a-b)(a+b)(b+c)(c+a)`
বীজগণিতের ঘন সূত্র
1. `(a+b)^3=a^3+3a^2b+3ab^2+b^3`
2. `(a-b)^3=a^3-3a^2b+3ab^2-b^3`
3. `(a-b)^3=a^3-b^3-3ab(a-b)`
4. `(a+b)^3=a^3+b^3+3ab(a+b)`
5. `a^3+b^3=(a+b)(a^2-ab+b^2)`
6. `a^3+b^3=(a+b)^3-3ab(a+b)`
7. `a^3-b^3=(a-b)(a^2+ab+b^2)`
8. `a^3-b^3=(a-b)^3+3ab(a+b)`
9. `a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)`
10. `a^3+b^3+c^3-3abc=\frac1{2}(a+b+c)\{(a-b)^2+(b-c)^2+(c+a)^2\}`
11. `\left(a+b+c\right)^3=a^3+b^3+c^3+3(a+b)(b+c)(c+a)`
12. `(a-b)^3+(b-c)^3+(c-a)^3=3(a-b)(b-c)(c-a)`
সূচক ও লগারিদমের সূত্র
1. `a^m\times a^n=a^{m+n}`
2. `\frac{a^m}{a^n}=a^{m-n}`
3. `(ab)^n=a^ma^n`
4. `\left(\frac ab\right)^n=\frac{a^n}{b^n}`
5. `\sqrt[m]{a^n}=a^\frac n{m}`
6. `a^\frac n{m}=a\left(\frac1{m}\right)^n`
7. `a^{-m}=\frac1{a^m}`
8. `\sqrt a=a^\frac1{2}`
9. `a^0=1`
10. `a^1=a`
11. `\log_a(MN)=\log_aM+\log_aN`
12. `\log_a(M\div N)=\log_aM-\log_aN`
13. `\log_ax=n` হলে `x=a^n`
14. `\log_aM^n=n\log_aM`
সমান্তর ধারার সূত্র
1. সমান্ত ধারার n তম পদ = a+(n-1)d
2. সমান্ত ধারার n সংখ্যক পদের সমস্টি `S_n=\frac n2\{2a+(n-1)d\}`
3. গুণোত্তর ধারার n তম পদ = `ar^{n-1}`
4. গুণোত্তর ধারার n সংখ্যক পদের সমস্টি `S_n=\frac{a(1-r^n)}{1-r}`
5.স্বাভাবিক সংখ্যার সমষ্টি = `\frac{n(n+1)}2`
6. বর্গের সমষ্টি = `\frac{n(n+1)(2n+1)}6`
7. ঘনের সমষ্টি = `{\frac{n(n+1)}2\}^2`
অফলাইনে অনুশীলন করার জন্য নিচের বীজগণিতের সূত্র সমূহ - এর ছবি ডাউনলোড করে নিতে পারেন।
 |
| বীজগণিতের সূত্র সমূহ |