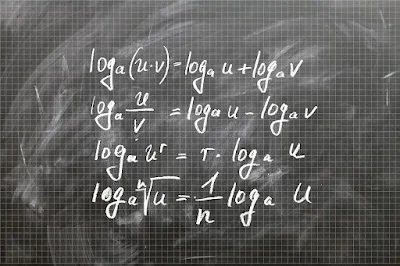 |
| সূচক ও লগারিদম |
সূচক ও লগারিদম
সূচক ও লাগারিদম - এর অংকগুলো সীমিত সংখ্যক সূত্র প্রয়োগ করে সমাধান করা হয় । তবে লগারিদমের সূত্র ব্যবহারের ক্ষেত্রে সাবধান না হলে লগারিদমের অংক গুলো সামাধানের ক্ষেত্রে সমস্যা হতে পারে ।
আর সূচক ও লগারিদমের অংক গুলোকে যাতে সহজে বুঝে উত্তর করা যায় সেজন্য সূচক ও লগারিদমের অংক এমন ভাবে নির্বাচন করা হয়েছে যেন প্রতিটি নিয়ম এর ভেতরে খুঁজে পাওয়া যায় । তবে প্রতিটি অংক শুধুমাত্র মুখস্ত না করে অবশ্যই বুঝে বার বার অনুশীলন করলে পরীক্ষায় ভালো ফলা পাওয়া যাবে । (ইনশাআল্লাহ)
আরো পড়তে পারেন
নবম - দশম শ্রেণির গণিত সৃজনশীল প্রশ্ন
এসএসসি বীজগণিত অংক সৃজনশীল : অধ্যায় ৩.১ - ৩.৪
লগারিদমের সূত্র
১. গুণ `a^m\times a^n=a^{m+n}`
২. ভাগ `\frac{a^m}{a^n}=a^{m-n}`
৩. গুণফলের ঘাত `(ab)^n=a^n\times b^n`
৪. ভাগফলের ঘাত `\left(\frac ab\right)^n=\frac{a^n}{b^n}`
৫. ঘাতের ঘাত `\left(a^m\right)^n=a^{mn}`
৬. শূন্য সূচক `a^0=1`
৭. ঋণাত্মক সূচক `a^{-n}=\frac1{a^n}`
৮. শূন্য লগ `\log_a1=0`
৯. এক লগ `\log_aa=1`
১০. গুণফলের লগ `\log_a\left(MN\right)=\log_aM+\log_nN`
১১. ভাগফলের লগ `\log_a\frac MN=\log_a-\log_aN`
১২. ঘাতের লগ `\log_aM^r=r\log_aM`
১৩. `\log_ab=\frac1{\log_ba}`
আরো পড়তে পারো
সূচক ও লগারিদম অংক সৃজনশীল প্রশ্ন
১. `a=\frac{x^p}{x^q}` `b=\frac{x^q}{x^r}` এবং `c=\frac{x^r}{x^p}`
ক. abc এর মান নির্ণয় কর ।
খ. প্রমাণ কর যে, `a^\frac1{pq}\times b^\frac1{qr}\times c^\frac1{rp}=1`
গ. দেখাও যে, `\left(p+q\right)\log a+\left(q+r\right)\log b+\left(r+p\right)\log c=0`
২. `A=X^p` , `B=X^q` , `C=X^r` এবং `M=2^{2x+1}`
ক. M=512 হলে X এর মান নির্ণয় কর ।
খ. `\left(\frac AB\right)^{p^2+pq+q^2}\times\left(\frac BC\right)^{q^2+qr+r^2}\times\left(\frac CA\right)^{r^2+rp+p^2}` এর মান নির্ণয় কর ।
গ. দেখাও যে, `\log_x\left(ABC\right)=\log_xA+\log_xB+\log_xC`
৩. `X=3^4.3^7\div3^9\times\frac1{81}` , `\sqrt[2]{7}\sqrt[3]{7}\div\sqrt[2]{7}` `Z=2^x+2^{1-x}=3`
ক. X এর মান নির্ণয় কর ।
খ. প্রমাণ কর যে, `Y-\sqrt[3]{7}=0`
গ. Z হতে X এর মান নির্ণয় কর ।
৪. `P^x=a` , `P^y=b` , `P^x=c`
ক. abc=P হলে প্রমাণ কর যে, x+y+z=1
খ. `\left(\frac ab\right)^{x^2+xy+y^2}\times\left(\frac bc\right)^{y^2+yz+z^2}\times\left(\frac ca\right)^{z^2+xz+x^2}` এর মান নির্ণয় কর ।
গ. প্রমাণ কর যে, `\left(\frac bc\right)^\frac1{yz}.\left(\frac ab\right)^\frac1{xy}.\left(\frac ca\right)^\frac1{xz}=1`
আরো পড়তে পারেন
৫. `P=\frac{2^{x+4}-4.2^{x+1}}{2^{x+2}\div2}` , `Q=\frac{3^{m+1}}{\left(3^m\right)^{m+1}}\div\frac{9^{m+1}}{\left(3^{m-1}\right)^{m+1}}` এবং `R=\frac{2^{q+1}.3^{2q-p}.5^{p+q}.6^p}{6^q.10^{p+2}.15^q}`
ক. `8^x=64` হলে x এর মান নির্ণয় কর ।
খ. P+Q এর মান নির্ণয় কর ।
গ. প্রমাণ কর যে, `R\times\sqrt{2500}=1`
৬. `A=\left(\frac{a^y}{a^z}\right)^{y^2+yz+z^2}` , `B=7^{x+1}` , `C=\left(\frac{a^x}{a^y}\right)^{x^2+xy+y^2}` , `D=\left(\frac{a^z}{a^x}\right)^{z^2+xz+x^2}` , `E=\frac{2^{x+4}-4.2^{x+1}}{2^{x+2}\div2}` , `F=\frac{3^{m+1}}{\left(3^m\right)^{m+1}}\div\frac{9^{m+1}}{\left(3^{m-1}\right)^{m+1}}`
ক. x এর কোন মানের জন্য B=49 হবে ?
খ. প্রমাণ কর যে, ACD=1
গ. দেখাও যে, `E\div F=36`
৭. a=2 , b=3 , c=5
ক. `\frac{b^{n+3}-5b^{n+1}}{b^{n+2}\div b}` এর মান নির্ণয় কর ।
খ. প্রমাণ কর যে, `\frac{a^{n+1}.b^{2n-m}.c^{m+n}.\left(ab\right)^m}{\left(ab\right)^n.\left(ac\right)^{m+2}.\left(bc\right)^n}=50`
গ. `\frac{\log\sqrt{b^3}+\log a^3-\log\sqrt{\left(ac\right)^3}}{\log a^2b-\log ac}` এর মান নির্ণয় কর ।
৮. `A=7\log_{10}\frac{10}9` , `B=2\log_{10}\frac{25}{24}` , `C=3\log_{10}\frac{81}{80}`
`a=\log_{2\sqrt5}400+\log_{3\sqrt2}324`
`b=\log_{49}7+\log_{2\sqrt5}20`
`c=\log_{12}\sqrt{12}+\log_24\sqrt2`
`d=\log_{10}40+\log_{10}\frac5{2}`
ক. `\log_x36=2` হলে x এর মান নির্ণয় কর ।
খ. A-B+C এর মান নির্ণয় কর ।
গ. প্রমাণ কর যে, a+c+d-b=`10\frac1{2}`
৯. `A=P^{x+y}` , `B=P^{y+x}` এবং `C=P^{z+x}`
ক. `\log_{3\sqrt2}324`এর মান নির্ণয় কর ।
খ. `\left(\frac AB\right)^{x+z}\times\left(\frac BC\right)^{y+x}\times\left(\frac CA\right)^{x+y}` এর মান নির্ণয় কর ।
গ. দেখাও যে, `\left(AB\right)^{x-z}\times\left(BC\right)^{y-x}\times\left(CA\right)^{x-y}=1`
১০. x=2 , y=3 , z=5 , w=7
ক. `\sqrt{y^3}` এর 3 ভিত্তিক লগ নির্ণয় কর ।
খ. `w\log\frac{xz}{y^2}-x\log\frac{z^2}{x^2y}+y\log\frac{y^4}{x^4z}` এর মান নির্ণয় কর ।
গ. দেখাও যে, `\frac{\log\sqrt{y^3}+y\log x-x\div y\log\left(xz\right)}{\log\left(xy\right)-\log z}=\log_y\sqrt{y^3}`
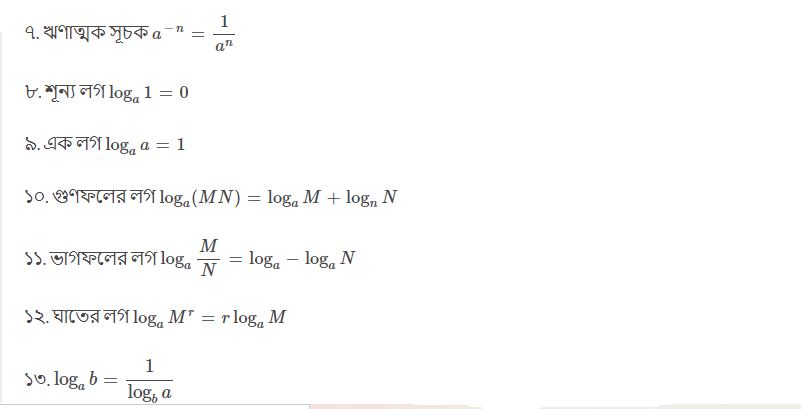 |
| লগারিদমের সূত্র |










এ গুলোর উত্তর দেন plz plz plZ🥹🥹🥹
উত্তরমুছুন