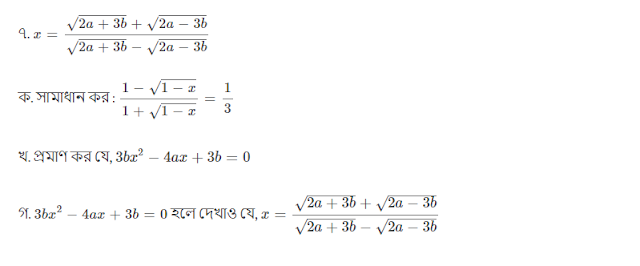অনুপাত ও সমানুপাতের ধারণা থাকা আমাদের জন্য খুবই গুরুত্বপূর্ণ । আমার প্রতিনিয়তই নির্মাণ সামগ্রী ও বিভিন্ন প্রকার খাদ্য সামগ্রী তৈরীতে , ভোগ্যপণ্য উৎপাদনে, জমিতে সার প্রয়োগে, কোনোও কিছুর আকার-আয়তন দৃষ্টিনন্দন করতে এবং দৈনিন্দিন কার্যক্রমের আরো অনেক ক্ষেত্রে অনুপাত ও সমানুপাতের ধারণা প্রয়োগ করা হয় ।
দশম শ্রেণির গণিত বইয়ের অধ্যায় ১১ : বীজগণিতীয় অনুপাত ও সমানুপাত অধ্যায় বীজণিতের অংশ । এছাড়াও যে কোনো প্রতিযোগীতামূলক পরীক্ষায় অনুপাত ও সমানুপাত থেকে অংক থাকে । বীজগণিতীয় অনুপাত ও সমানুপাত অধ্যায় বিশ্লেষণ করে অনুপাতের অংক সৃজনশীল প্রশ্ন এমন ভাবে তৈরি করা হয়েছে যেন অনুপাত ও সমানুপাতের সকল নিয়মগুলো এর মধ্যে অন্তর্ভূক্ত থাকে ।
আরো পড়তে পারেন
যাতে এ অধ্যায় থেকে যে কোনো সৃজনশীল প্রশ্ন আসলে শিক্ষার্থীরা সহজেই উত্তর প্রদান করতে সক্ষম হয় । এছাড়াও এ আর্টিকেলে অনুপাত কি?, সমানুপাত কি?, অনুপাতের প্রকার সমূহ এবং অনুপাত করার নিয়মগুলো সম্পর্কে বিস্তারিত আলোচনা করা হয়েছে । যাতে অনুপাত ও সমানুপাত অংত করতে গিয়ে শিক্ষার্থীরা এ সমন্ধে বিস্তারিত ধারনা লাভ করতে পারে ।
অনুপাত ( Ratio ) কাকে বলে ? বা অনুপাত কী ?
একই
এককে সমজাতীয় দুইটি রাশির পরিমাণের একটি অপরটির কত
গুণ বা কত অংশ
তা একটি ভগ্নাংশ দ্বারা
প্রকাশ করা যায় ।
এ ভগ্নাংশকে রাশি দুইটির অনুপাত ( Ratio ) বলে ।
অনুপাতের প্রকার সমূহ
দুইটি
রাশি p ও q এর অনুপাতকে
p : q = `\frac p{q}` লেখা
হয় । যেখানে p ও
q দুইটি সমজাতীয় এবং একই এককে
প্রকাশিত । এখানে p কে
পূর্ব রাশি ও q কে
উত্তর রাশি বলে ।
সমতুল
অনুপাত : যে অনুপাতের পূর্ব
ও উত্তর রাশি কে শূন্য
( ০ ) ব্যাতীত যে কোনো সংখ্যা
দ্বারা ভাগ করলে অনুপাতের
মানের কোনো পরিবর্তন হয়
না তাকে সমতুল অনুপাত
বলে ।
সরল
অনুপাত : যে অনুপাতে কেবল
মাত্র দুটি রাশি থাকে
তাকে সরল অনুপাত বলে
। যেমন : ৩ : ৫
লঘু
অনুপাত : যে অনুপাতের পূর্ব
রাশি উত্তর রাশি থেকে ছোট
তাকে লঘু অনুপাত বলে
। যেমন : ৩ : ৫
গুরু
অনুপাত : যে অনুপাতের পূর্ব
রাশি ুউত্তর রাশি থেকে বড়
তাকে গুরু অনুপাত বলে
। যেমন : ৫ : ৩
একক
অনুপাত : যে সরল অনুপাতের
পূর্ব রাশি ও উত্তর
রাশি সমান তাকে একক
অনুপাত বলে । যেমন
: ৫ : ৫
ব্যস্ত অনুপাত : কোনো অনুপাতের পূর্ব রাশিকে উত্তর রাশি এবং উত্তর রাশি কে পূর্ব রাশি করা হলে নতুন যে অনুপাত তৈরি হয় তাকে ব্যস্ত অনুপাত বলে । যেমন : ৭ : ৮ এর ব্যস্ত অনুপাত ৮ : ৭
মিশ্র অনুপাত : একাধিক সরল অনুপাতের পূর্ব রাশির গুণফলকে পূর্ব রাশি এবং উত্তর রাশির গুণফল কে উত্তর রাশি ধরে যে অনুপাত পাওয়া যায় তাকে মিশ্র অনুপাত বলে । যেমন : ৫ :৩ এবং ১ : ২ এর মিশ্র অনুপাত ৫×১ : ৩×২ = ৫ : ৬
বহু রাশিক অনুপাত : তিন বা ততোধিক রাশির অনুপাতকে বহুরাশিক অনুপাত বলে । যেমন : ৮ : ৫ : ৩
ধারাবাহিক অনুপাত : দুটি ভিন্ন অনুপাতকে ধারাবাহিক ভাবে প্রকাশ করাকে ধারাবাহিক অনুপাত বলে । যেমন : ক : খ = ১ : ২ এবং খ : গ = ৩ : ৪ এদের ধারাবাহিক অনুপাত প্রকাশ করলে হয় = ১ × ৩ : ২ × ৩ = ৩ : ৬ এবং ৩ × ২ : ৪ × ২ = ৬ : ৮
∴ এদের
ধারাবাহিক অনুপাত = ৩ : ৬ : ৮
আরো পড়তে পারেন
সমানুপাতিক কাকে বলে
যদি চারটি রাশি এরূপ হয় যে, প্রথম ও দ্বিতীয় রাশির অনুপাত তৃতীয় ও চতুর্থ রাশির অনুপাতের সমান হয় তবে এ ধরনের রাশিকে সমানুপাত ( Proportion ) বলে । সমানুপাতের প্রত্যেক রাশিকে সমানুপাতী বা সমানুপাতিক বলে ।
ত্রৈরাশিক
কাকে বলে ?
সমানুপাতের তিনটি রাশি জানা থাকলে ৪র্থ রাশি নির্ণয় করা যায় । এই ৪র্থ রাশি নির্ণয় করার পদ্ধতিকে ত্রৈরাশিক বলে
ক্রমিক সমানুপাত
তিনটি
রাশির ১ম ও ২য়
রাশির অনুপাত এবং ২য় ও
৩য় রাশির অনুপাত পরস্পর সমান হলে সমানুপাতটিকে
ক্রমিক সমানুপাত বলে । রাশি
তিনটিকে ক্রমিক সমানুপাতী বলে ।
অনুপাতের সূত্র
ত্রৈরাশিক
সূত্র : ১ম রাশি × ৪র্থ
রাশি = ২য় রাশি × ৩য়
রাশি
অনুপাতের
একটি অংশের পরিমান = প্রদত্ত রাশি × ( ঐ অনুপাতের সংখ্যা
÷ অনুপাতের রাশি গুলোর যোগফল
)
এছাড়াও
অনুপাত বিভিন্ন প্রক্রিয়া অনুপাতের রূপান্তর করা
১. ব্যস্তকরণ যেমন : a : b = c : d এর ব্যস্তকরণ b : a = d : c
2. একান্তরকরণ
যেমন : a : b = c : d এর একান্তরকরণ a : c = b : d
৩. যোজন যেমন : a : b = c : d এর যোজন
`\frac{a+b}b=\frac{c+d}d`
৪. বিয়োজন যেমন : a : b = c : d এর বিয়োজন `\frac{a-b}b=\frac{c-d}d`
৫. যোজন - বিয়োজন যেমন : a : b = c : d এর যোজন - বিয়োজন
`\frac{a+b}{a-b}=\frac{c+d}{c-d}`
আরো পড়তে পারেন
সূচক ও লগারিদম অংক সৃজনশীল এবং লগারিদমের সূত্র : ( ৪.১ - ৪.৩ )
অনুপাতের অংক
১. `\frac{\sqrt{1+x}+\sqrt{1-x}}{\sqrt{1+x}-\sqrt{1-x}}=p`
ক. `\frac{a^3+b^3}{a-b+c}=a(a+b)`
হলে প্রমাণ কর যে, a, b, c ক্রমিক
সমানুপাতি ।
খ. উদ্দীপকের আলোকে প্রমাণ কর যে , `p^2-\frac{2p}x+1=0`
২. a, b, c ক্রমিক সমানুপাতি ।
ক. প্রমাণ কর যে, `\frac{abc(a+b+c)^3}{(ab+bc+ca)^3}=1`
খ. প্রমাণ কর যে, `\frac{a^2+b^2}{b^2+c^2}=\frac{(a+b)^2}{(b+c)^2}`
গ. `\frac{a^2+b^2}{b^2+c^2}=\frac{(a+b)^2}{(b+c)^2}` হলে দেখাও যে, a, b, c ক্রমিক সমানুপাতি ।
৩. a, b, c, d ক্রমিক সমানুপাতি ।
ক. প্রমাণ কর যে, `\frac{a^3+b^3}{b^3+c^3}=\frac{b^3+c^3}{c^3+d^3}`
খ. দেখাও যে, `(a^2+b^2+c^2)(b^2+c^2+d^2)=(ab+bc+cd)^2`
গ. সামাধান কর : `\frac{1-ax}{1+ax}\sqrt{\frac{1+bx}{1-bx}}=1`
৪. `x=\frac{4ab}{a+b}`
ক. a,
b, c ক্রমিক সমানুপাতি হলে প্রমাণ কর
যে, `\frac
a{c}=\frac{a^2+b^2}{b^2+c^2}`
খ. দেখাও যে, `\frac{x+2a}{x-2a}+\frac{x+2b}{x-2b}=2`
গ. `\frac{x+2a}{x-2a}+\frac{x+2b}{x-2b}=2` হলে প্রমাণ কর যে, `a^{-1}+b^{-1}=2x^{-1}`
৫. `\frac{6}{y}=\frac1{p}+\frac1{q}`
ক. দেখাও যে, `y=\frac{6pq}{p+q}`
খ. প্রমাণ কর যে, `\frac{y+3p}{y-3p}+\frac{y+3q}{y-3q}=2`
গ. সমাধান কর : `\frac{a+x-\sqrt{a^2-x^2}}{a+x+\sqrt{a^2-x^2}}=\frac b{x}` যেখানে 2a>b>0
আরো পড়তে পারেন
৬. `x^3-3mx^2+3x-m=0`
ক. a, b, c, d ক্রমিক সমানুপাতি হলে প্রমাণ কর যে, `a-2b+c=\frac{(a-b)^2}a=\frac{(b-c)^2}c`
গ. হলে প্রমাণ
কর যে , `x^3-3mx^2+3x-m=0`
৭. `x=\frac{\sqrt{2a+3b}+\sqrt{2a-3b}}{\sqrt{2a+3b}-\sqrt{2a-3b}}`
ক. সামাধান কর
: `\frac{1-\sqrt{1-x}}{1+\sqrt{1-x}}=\frac1{3}`
খ. প্রমাণ কর যে, `3bx^2-4ax+3b=0`
গ. `3bx^2-4ax+3b=0` হলে দেখাও যে, `x=\frac{\sqrt{2a+3b}+\sqrt{2a-3b}}{\sqrt{2a+3b}-\sqrt{2a-3b}}`
৮. a=x+y+z, b=y+z-x, c=z+x-y, d=x+y-z
ক. দুইটি সংখ্যার অনুপাত 5 : 7 এবংএদের গ.সা.গু
হলে, সংখ্যা দুইটির ল.সা.গু
নির্ণয় কর।
খ. `\frac
b{y+z}=\frac c{z+x}=\frac d{x+y}` হলে
প্রমাণ কর যে, x=y=z
গ. ap=bq=cr=ds হলে দেখাও যে, `\frac 1{q}=\frac 1{r}=\frac 1{s}=\frac 1{p}`
৯. একটি জমির ক্ষেত্রফল 192 বর্গ মিটার জমিটির দৈর্ঘ্য 4 মিটার কমালে এবং প্রস্থ 4 মিটার বাড়ালে ক্ষেত্রফল অপরিবর্তিত থাকে ।
ক. জমিটির দৈর্ঘ্য x এবং প্রস্থ y ধরে
সমীকরণ নির্ণয় কর ।
খ. জমিটির পরিসীমা নির্ণয় কর ।
গ. জমিটির দৈর্ঘ্য 10% বৃদ্ধি এবং প্রস্থ 10% হ্রাস পেলে ক্ষেত্রফল শতকরা কত হ্রাস বা বৃদ্ধি হবে ?
আরো পড়তে পারেন
১০. (i) `p=\frac{4mn}{m+n}` (ii) `\frac6{a}=\frac1{x}+\frac1{y}`
ক. `\frac{p+1}{p-1}`
এর মান নির্ণয় কর
।
খ. (i)
হতে দেখাও যে, `\frac{p+2m}{p-2m}+\frac{p+2n}{p-2n}=2`
গ. (ii) ব্যবহার করে , `\frac{a+3x}{a-3x}+k=\frac{a+3y}{a-3y}` হলে k এর মান নির্ণয় কর ।
১১. একটি আয়তকার জমির ক্ষেত্রফল 12 হেক্টর এবং কর্ণের দৈর্ঘ্য 500 মিটার । ঐ জমির দৈর্ঘ্য ও প্রস্থের সঙ্গে অপর একটি জমির দৈর্ঘ্য ও প্রস্থের অনুপাত যথাক্রমে 3 : 4 এবং 2 : 3 ।
ক. প্রদত্ত আয়তকার জমিটির ক্ষেত্রফল কত বর্গমিটার ।
খ. অপর জমিটির ক্ষেত্রফল
নির্ণয় কর ।
গ. প্রদত্ত জমিটির প্রস্থ নির্ণয় কর ।
অফলাইনে অনুশীলন করার জন্য নিচ থেকে অনুপাতের অংক গুলোর ছবি ডাউনলোড করে নিতে পারো
 |
| অনুপাতের অংক |
আশা করি সমানুপাত ও অনুপাতের অংক সৃজনশীল প্রশ্ন তোমাদের উপকারে আসবে । ভালো লাগলে বন্ধুদের সাথে শেয়ার করে তাদেরকেও জানার সুযোগ করে দিও । এছাড়াও আরো কোনো বিষয় জানার প্রয়োজন হলে আমাদের প্রশ্ন করতে পারো । আমার চেষ্টা করো শিঘ্রই তোমাদের প্রশ্নগুলোর উত্তর প্রদান করতে ।
আরো পড়তে পারেন
তাহলে কি আমাদের ঘুমের কোন প্রয়োজন নেই !