পরিসংখ্যান অংক
এস এস পরীক্ষায় গণিতে পরিসংখ্যান অংক থেকে ২ টি সৃজনশীল প্রশ্ন থাকে যার মধ্যে একটি প্রশ্নের উত্তর করা বাধ্যতা মূলক । পরিসংখ্যান থেকে প্রশ্নের উত্তর করতে সময় বেশি লাগলেও এটির উত্তর করা সহজ । গড়, মধ্যক, প্রচুরক, আয়তলেখ, অজিভরেখা, গণসংখ্যা বহুভুজ মাত্র ৬ টি বিষয় শিখলেেই ১০ নম্বর ১০০% কমন । তাই আজকের আর্টিকেলের মাধ্যমে আমরা সহজ পদ্ধতিতে পরিসংখ্যান অংক করার নিয়ম বর্ণনা করেছি । আশা করি ছাত্র - ছাত্রীদের উপকারে আসবে ।
এছাড়াও আমাদের বাস্তব জীবনেও পরিসংখ্যান অংক - এর ব্যবহার রয়েছে । তাই এটি সম্পর্কে জ্ঞান থাকা প্রত্যেক শিক্ষার্থীর জন্য আবশ্যক ।
 |
| পরিসংখ্যান অংক |
এ আর্টিকেলে আপনার যে অংশ জানার প্রয়োজন সেখানে ক্লিক করে জেনে নিন ।
পরিসংখ্যান কাকে বলে
পরিসংখ্যান শব্দটির ইংরেজি Statistic । পরিসংখ্যান হলো এক ধরনের সংখ্যা বিজ্ঞান যা মূলত উপাত্ত সংগ্রহ, বিশ্লেষন, ব্যাখ্যা ও উপাত্ত সহজে পরিবেশন নিয়ে কাজ করে ।
উপাত্ত দুই প্রকার । যথা : ১. বিন্যস্ত ২. অবিন্যস্ত উপাত্ত
বিন্যস্ত উপাত্ত : যে উপাত্তগুলো কোনো বৈশিষ্ট্য অনুযায়ী বিভিন্ন শ্রেণিতে সাজানো থাকে সেগুলোকে বিন্যস্ত উপাত্ত বলে।
অবিন্যস্ত উপাত্ত : যে উপাত্তগুলো কোনো বৈশিষ্ট্য অনুযায়ী সাজানো থাকে না তাকে অবিন্যস্ত উপাত্ত বলে।
গড় নির্ণয়ের পদ্ধতি
এক জাতীয় একাধিক রাশির সমষ্টিকে রাশিগুলোর মোট সংখ্যা দ্বারা ভাগ করল যে ভাগফল পাওয়া যায় তাকে গড় বলে ।
গড় তিন প্রকারে নির্ণয় করা যায় । যথা : ১. সরাসির গড় ২. গাণিতিক গড় ৩. সংক্ষিপ্ত পদ্ধতিতে গড়
সরাসরি গড় নির্ণয়ের পদ্ধতি
সরাসির রাশির গুলোকে যোগ করে রাশির সংখ্যা দ্বারা ভাগ করলে যে ভাগফল পাওয়া যায় তাই সরাসরি গড় । যেমন : ২, ৩, ৪, এর সরাসরি গড় = (২+৩+৪ ) ÷ ৩ = ৩
সংক্ষিপ্ত পদ্ধতিতে গড় নির্ণয়ের নিয়ম
| শ্রেণি |
11 - 20 |
21 - 30 |
31 - 40 |
41 - 50 |
| গণসংখ্যা |
4 |
16 |
20 |
25 |
সংক্ষিপ্ত পদ্ধতিতে গড় নির্ণয়ের সারণি হবে নিম্নরূপ :
| শ্রেণি ব্যাপ্তি |
মধ্যমান xi |
গণসংখ্যা fi |
ধাপ বিচ্যুতি ui = `\frac{xi-a}h` |
fiui |
| 11 - 20 |
15.5 |
4 |
-1 |
-4 |
| 21 - 30 |
25.5 a |
16 |
0 |
0 |
| 31 - 40 |
35.5 |
20 |
1 |
20 |
| 41 - 50 |
45.5 |
25 |
2 |
50 |
| মোট |
|
65 |
|
66 |
এখানে,
a = 25.5 , ∑fiui = 66, n = 65 , h = 10
আমরা জানি,
গাণিতিক গড় = `a+\frac{\sum fiui}n\times h`
∴ গাণিতিক গড় = `25.5+\frac{66}{65}\times10`
= 35.65 ( প্রায় )
গাণিতিক গড় নির্ণয়ের পদ্ধতি
গাণিতিক পদ্ধতিতে গড় নির্ণয়ের সারণি হবে নিম্নরূপ :
| শ্রেণি ব্যাপ্তি |
মধ্যমান xi |
গণসংখ্যা fi |
fixi |
| 11 - 20 |
15.5 |
4 |
62 |
| 21 - 30 |
25.5 |
16 |
408 |
| 31 - 40 |
35.5 |
20 |
710 |
| 41 - 50 |
45.5 |
25 |
1137.5 |
| মোট |
|
65 |
2317.5 |
এখানে,
n = 65
∑fiui = 2317.5
আমরা জানি,
গাণিতিক গড় = `\frac1{n}\times\sum fixi`
∴ গাণিতিক গড় = `\frac1{65}\times2317.5`
= 35.65
মধ্যক নির্ণয়ের পদ্ধতি
পরিসংখ্যানের উপাত্তগুলোকে মানের ক্রমানুসারে সাজালে যে মান উপাত্তগুলোকে সমান দুই ভাগে ভাগ করে সে মানই হলো উপাত্তগুলোর মধ্যক । মধ্যক দুই প্রক্রিয়ায় নির্ণয় করা যায়
i) অবিন্যস্ত উপাত্তের মধ্যক
ii) বিন্যস্ত উপাত্তের মধ্যক
অবিন্যস্ত উপাত্তের মধ্যক নির্ণয়ের পদ্ধতি
মনে করি,
উপাত্তের সংখ্যা = n
এখন n যদি জোড় হয় তাহলে মধ্যক = { `\frac{n}{2}` তম পদ + (`\frac{n}{2}+1`) তম পদ } ÷ 2
যেমন : 23, 11, 25, 21, 12, 17
উপাত্তগুলোকে মানের ক্রমানুসারে সাজালে = 11, 12, 17, 21, 23, 25
এখনে n = 6 । যা জোড় সংখ্যা
∴ মধ্যক = { `\frac{6}{2}` তম পদ + (`\frac{6}{2}+1`) তম পদ } ÷ 2
= ( 3 তম পদ + 4 তম) ÷ 2
= ( 17+21 ) ÷ 2
= 19
আবার, উপাত্তের সংখ্যা = n
এখন n যদি বিজোড় হয় তাহলে মধ্যক = `\frac{n+1}2` তম পদ
যেমন : 23, 11, 25, 21, 12
উপাত্তগুলোকে মানের ক্রমানুসারে সাজালে = 11, 12, 21, 23, 25
এখনে n = 5 । যা বিজোড়
∴ মধ্যক = `\frac{5+1}2` তম পদ
= 3 তম পদ
= 21
বিন্যস্ত উপাত্তের মধ্যক নির্ণয়ের পদ্ধতি
| শ্রেণি |
11 - 20 |
21 - 30 |
31 - 40 |
41 - 50 |
| গণসংখ্যা |
4 |
16 |
20 |
25 |
মধ্যাক নির্ণয়ের সারণি হবে নিম্নরূপ :
| শ্রেণি ব্যাপ্তি |
গণসংখ্যা |
ক্রমোযোজিত গণসংখ্যা |
| 11 - 20 |
4 |
4 |
| 21 - 30 |
16 |
20 |
| 31 - 40 |
20 |
40 |
| 41 - 50 |
25 |
65 |
| মোট |
n = 65 |
|
এখানে,
n = 65
মধ্যক = `\frac{n}2` তম পদ
= `\frac{65}2` তম পদ
= 32.5 তম পদ
32.5 তম পদ ( 31 - 40 ) এর মধ্যে অবস্থিত । সুতরাং মধ্যক ( 31 - 40 ) এর মধ্যে অবস্থিত
মধ্যক শ্রেণির নিম্নসীমা L = 31
মধ্যক শ্রেণির পূর্ববর্তী শ্রেণির ক্রমযোজিত গণসংখ্যা Fc = 20
মধ্যক শ্রেণির গণসংখ্যা fm = 20
শ্রেণি ব্যবধান h = 10
উপাত্তগুলোর সংখ্যা n = 65
আমরা জানি,
মধ্যক = `L+(\frac{n}2-Fc)\times\frac h{fm}`
∴ মধ্যক = `31+(\frac{65}2-20)\times\frac{10}{20}`
= 37.25
আরো পড়তে পারেন
প্রচুরক নির্ণয়ের পদ্ধতি
কোনো উপাত্তে যে সংখ্যাটি সবচেয়ে বেশি বার থাকে তাকে প্রচুরক বলে । মধ্যকের মতো প্রচুরকও দুটি পদ্ধতিতে নির্ণয় করা হয় ।
i) অবিন্যস্ত উপাত্তের প্রচুরক
ii) বিন্যস্ত উপাত্তের প্রচুরক
অবিন্যস্ত উপাত্তের প্রচুরক নির্ণয়ের পদ্ধতি
5, 3, 4, 6 ,3 এখানে 3 সংখ্যাটি দুই বার রয়েছে । যা সবচেয়ে বেশি । সুতরাং প্রচুরক 3 ।
বিন্যস্ত উপাত্তের প্রচুরক নির্ণয়ের পদ্ধতি
| শ্রেণি |
11 - 20 |
21 - 30 |
31 - 40 |
41 - 50 |
| গণসংখ্যা |
4 |
16 |
20 |
25 |
প্রচুরক নির্ণয়ের সারণি হবে নিম্নরূপ :
| শ্রেণি |
11 - 20 |
21 - 30 |
31 - 40 |
41 - 50 |
| গণসংখ্যা |
4 |
16 |
20 |
25 |
এখানে,
গণসংখ্যা ২৫ সবচেয়ে বেশি । যা ( 41 - 50 ) এর মধ্যে অবস্থিত । সুতরাং ( 41 - 50 ) এর মধ্যে প্রচুরক বিদ্যমান ।
প্রচুরক শ্রেণির নিম্নসীমা L = 41
প্রচুরক শ্রেণির গণসংখ্যা ও তা পূর্ববর্তী শ্রেণির গণসংখ্যার পার্থক্য `f_1` = 25 - 20 = 5
প্রচুরক শ্রেণির গণসংখ্যা ও তার পরবর্তী শ্রেণির গণসংখ্যার পার্থক্য `f_2` = 25 - 0 = 25
আমরা জানি,
প্রচুরক = `L+\frac{f_1}{f_1+f_2}\times h`
∴ প্রচুরক = `41+\frac5{5+25}\times10`
= 42.67 ( প্রায় )
আরো পড়তে পারেন
আয়তলেখ অঙ্কনের পদ্ধতি
অবিচ্ছিন্ন গণসংখ্যা সারণির লেখচিত্রকে আয়তলেখ বলে।
| শ্রেণি |
11 - 20 |
21 - 30 |
31 - 40 |
41 - 50 |
| গণসংখ্যা |
4 |
16 |
20 |
25 |
আয়তলেখ অঙ্কের সারণি নিম্নরূপ
| শ্রেণি ব্যাপ্তি |
অবিচ্ছিন্ন শ্রেণি ব্যাপ্তি | গণসংখ্যা |
| 11 - 20 |
10.5 - 20.5 |
4 |
| 21 - 30 |
20.5 - 30.5 |
16 |
| 31 - 40 |
30.5 - 40.5 |
20 |
| 41 - 50 |
40.5 - 50.5 |
25 |
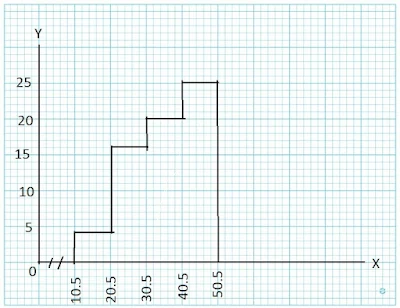
ছক কাগজে x ও y অক্ষ আঁকি । x অক্ষ বরাবর অবিচ্ছিন্ন শ্রেণি ব্যাপ্তি প্রতি ক্ষৃদ্র বর্গ ঘরকে ২ একক ধরে এবং y অক্ষ বরাবর গণসংখ্যা প্রতি ক্ষৃদ্র বর্গ ঘরকে ১ একক ধরে আয়তলেখ আঁকা হলো :
অজিভরেখা অঙ্কনের পদ্ধতি
কোনো উপাত্তের শ্রেণি বিন্যাসের পর শ্রেণি ব্যবধানের উচ্চসীমা x অক্ষ বরাবর এবং শ্রেণির ক্রমযোজিত গণসংখ্যা y অক্ষ বরাবর স্থাপন করে অজিভ রেখা পাওয়া যায় ।
| শ্রেণি |
11 - 20 |
21 - 30 |
31 - 40 |
41 - 50 |
| গণসংখ্যা |
4 |
16 |
20 |
25 |
আরো পড়তে পারেন
অজিভ রেখা অঙ্কনের সারণি হবে নিম্নরূপ :
| শ্রেণি ব্যাপ্তি |
অবিচ্ছিন্ন শ্রেণি ব্যাপ্তি |
গণসংখ্যা |
ক্রমযেজিত গণসংখ্যা |
| 11 - 20 |
10.5 - 20.5 |
4 |
4 |
| 21 - 30 |
20.5 - 30.5 |
16 |
20 |
| 31 - 40 |
30.5 - 40.5 |
20 |
40 |
| 41 - 50 |
40.5 - 50.5 |
25 |
65 |
ছক কাগজে x ও y অক্ষ আঁকি । x অক্ষ বরাবর অবিচ্ছিন্ন শ্রেণি ব্যাপ্তি প্রতি ক্ষৃদ্র বর্গ ঘরকে ২ একক ধরে এবং y অক্ষ বরাবর ক্রমযোজিত গণসংখ্যা প্রতি ক্ষৃদ্র বর্গ ঘরকে ২ একক ধরে অজিভ রেখা আঁকা হলো :
আরো পড়তে পারেন
গণসংখ্যা বহুভুজ অঙ্কনের পদ্ধতি
অবিচ্ছিন্ন উপাত্তের শ্রেণি ব্যবধানের বিপরীত গণসংখ্যা নির্দেশক বিন্দুসমূহকে পর্যায়ক্রমে রেখাংশ দ্বারা যুক্ত করে যে লেখচিত্র পাওয়া যায় তাকেই গণসংখ্যা বহুভুজ বলে।
| শ্রেণি |
11 - 20 |
21 - 30 |
31 - 40 |
41 - 50 |
| গণসংখ্যা |
4 |
16 |
20 |
25 |
গণসংখ্যা বহুভুজ অঙ্কনের সারণি নিম্নরূপ :
| শ্রেণি ব্যাপ্তি |
মধ্যমান |
গণসংখ্যা |
| 11 - 20 |
15.5 |
4 |
| 21 - 30 | 20.5 |
16 |
| 31 - 40 |
30.5 |
20 |
| 41 - 50 |
40.5
| 25 |
ছক কাগজে x ও y অক্ষ আঁকি । x অক্ষ বরাবর মধ্যমান প্রতি ক্ষৃদ্র বর্গ ঘরকে ২ একক ধরে এবং y অক্ষ বরাবর গণসংখ্যা প্রতি ক্ষৃদ্র বর্গ ঘরকে ১ একক ধরে অজিভ রেখা আঁকা হলো :
আশা করি দশম শ্রেণির পরিসংখ্যান অংক তোমাদের উপকারে আসবে । ভালো লাগলে বন্ধুদের সাথে শেয়ার করে তাদেরকেও জানার সুযোগ করে দিও । এছাড়াও আরো কোনো বিষয় জানার প্রয়োজন হলে আমাদের প্রশ্ন করতে পারো । আমার চেষ্টা করো শিঘ্রই তোমাদের প্রশ্নগুলোর উত্তর প্রদান করতে ।
আরো পড়তে পারেন