খ্রিষ্টপূর্ব ৩০০ অব্দের কাছাকাছি সময় গ্রিকে এমন একজন গণিতজ্ঞের আবির্ভাব হয় যাকে নিঃসন্দেহে পৃথিবীর সবচেয়ে জনপ্রিয় গণিত বইয়ের প্রণেতা বলা যায় । তিনি স্বনাম ধন্য ইউক্লিড, তার পুস্তকের নাম Elements । তিনি অশেষ ধৈর্য্য সহকারে তৎকালীন সমুদয় জ্যামিতিক জ্ঞান সম্পদ সংগ্রহ করে সেগুলোকে যথাযথ ক্রমানুসারে সাজিয়ে প্রণয়ন করেন বিখ্যাত জ্যামিতি - এর গ্রন্থ Elements । প্রায় দুই হাজার বছর ধরে এই গ্রন্থ বিশ্বের কোটি কোটি শিক্ষার্থীর জ্যামিতি শেখার আকর গ্রান্থ হিসেবে প্রতিষ্ঠিত ।
আমাদের দৈনিন্দিন প্রায় সকল কাজে জ্যামিতি - এর ব্যবহার রয়েছে । আধুনিক কালে গণিত, বিজ্ঞান সহ জ্ঞানের প্রায় সকল শাখায় জ্যামিতির ব্যবহার রয়েছে ।
আজকের আর্টিকেলে আমরা জ্যামিতি শেখার প্রাথমিক সকল বিষয়গুলোর সংজ্ঞাসহ চিত্র উপস্থাপন করেছি । আশা করি শিক্ষার্থীদের উপকারে আসবে ।
জ্যামিতি কাকে বলে
জ্যামিতি শব্দটি দুটি গ্রীক শব্দের সমন্বয়ে গঠিত । এর মধ্যে জ্যা অর্থ জমি এবং মিতি অর্থ পরিমাপ অর্থ্যাৎ জ্যামিতি অর্থ জমির পরিমাপ ।
যে বিষয় পাঠ করলে জমির পরিমাপ প্রণালী সমন্ধে জানা যায় তাকে জ্যামিতি বলে । তবে বর্তমান কালে জ্যামিতি গণিতের বিভিন্ন শাখায় ব্যবহার করা হয় । জ্যামিতিক জ্ঞান কাজে লাগিয়ে আধুনিক কালে বিভিন্ন সমস্যার সমাধান করা হয় ।
আরো পড়তে পারেন
বিন্দু কাকে বলে
যার দৈর্ঘ্য, প্রস্থ, মাত্রা নেই কিন্তু অবস্থান আছে তাকে বিন্দু বলে ।
 |
| চিত্র : A একটি বিন্দু |
মধ্যবিন্দু কাকে বলে
যে বিন্দু একটি সরল রেখাকে সমান দু ভাগে বিভক্ত করে তাকে মধ্যবিন্দু বলে ।
 |
| চিত্র : O হলো AB সরলরেখার মধ্যবিন্দু |
রেখা কাকে বলে
বিন্দু চলার পথকে রেখা বলে ।
 |
| চিত্র : AB একটি রেখা |
বক্ররেখা কাকে বলে
যে রেখা চলার পথে দিক পরিবর্তন করে তাকে বক্ররেখা বলে।
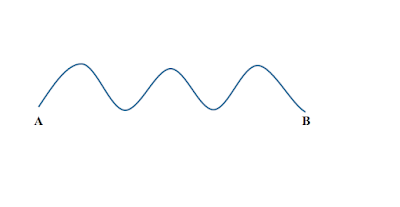 |
| চিত্র : AB একটি বক্ররেখা |
রেখাংশ কাকে বলে
কোনো একটি রেখার দুইটি বিন্দু নির্দিষ্ট করলে তাদের দ্বারা সীমাবদ্ধ রেখার অংশকে রেখাংশ বলে ।
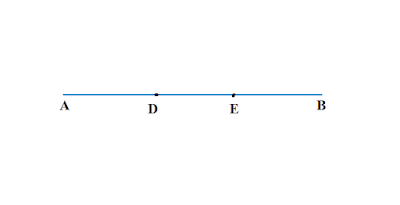 |
| চিত্র : DE হলো AB এর একটি রেখাংশ |
সমান্তরাল রেখা কাকে বলে
যদি দুইটি সরল রেখা পরস্পরকে কোথাও ছেদ না করে সর্বদা সমান দূরত্ব বজায় রেখে অবস্থান করে, তবে ঐ রেখা দুইটিকে সমান্তরাল রেখা বলে ।
 |
| চিত্র : AB ও CD পরস্পর সমান্তরাল রেখা |
রশ্মি কাকে বলে
যদি রেখাংশের একটি প্রান্ত বিন্দুর অবস্থান স্থির থাকে এবং অপর বিন্দুর অবস্থান সীমাহীনভাবে যথেচ্ছা বাড়িয়ে দেওয়া যায়, তবে তাকে রশ্মি বলে ।
 |
| চিত্র : AB একটি রশ্মি |
পরস্পরচ্ছেদী রেখা কাকে বলে
দুইটি সরলরেখা একই বিন্দু দিয়ে পপরস্পরকে অতিক্রম করলে তাকে পরস্পরচ্ছেদী রেখা বলে ।
 |
| চিত্র : AB ও CD পরস্পরচ্ছেদী রেখা |
ছেদক কাকে বলে
একটি রেখা অপর একটি রেখাকে যে কোনো একটি বিন্দুতে ছেদ করলে প্রথমোক্ত রেখাটিকে দ্বিতীয় রেখার ছেদক বলে ।
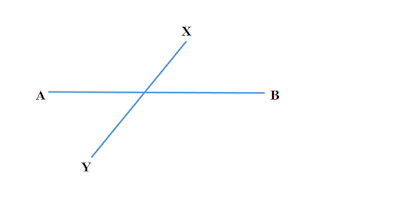 |
| চিত্র : XY, AB এর ছেদক |
লম্ব দ্বিখন্ডক কাকে বলে
যদি একটি রেখাকে অপর একটি রেখা সমকোণে সমদ্বিখন্ডিত করে তবে তাকে লম্ব দ্বিখন্ডক বলে ।
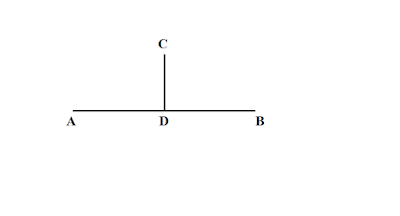 |
| চিত্র : CD রেখা AB রেখার লম্ব দ্বিখন্ডক |
লম্ব কাকে বলে
একটি সরলরেখা অপর একটি সরলরেখার উপর দন্ডায়মান হয়ে যদি সমকোণ উৎপন্ন করে তবে তাকে লম্ব বলে ।
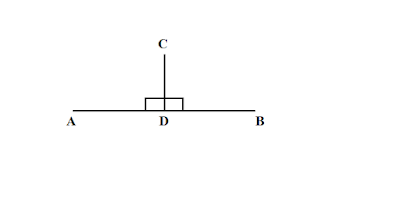 |
| চিত্র : AB রেখার উপর CD লম্ব |
কোণ কাকে বলে
যদি দুইটি সরলরেখা একই বিন্দতে মিলিত হয়, তবে মিলিত স্থানকে কোণ বলে ।
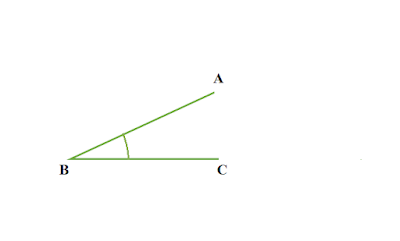 |
| চিত্র : ABC একটি কোণ |
সন্নিহিত কোণ কাকে বলে
যদি দুইটি কোণের একই শীর্ষবিন্দু ও একটি সাধারণ বাহু এবং কোণ দুইটি সাধারণ বাহুর বিপরীত পার্শ্বে অবস্থিত হয় , তবে ঐ কোণ দুইটিকে একে অপরের সন্নিহিত কোণ বলে ।
 |
| চিত্র : ∠ABC এবং ∠DBC পরস্পর সন্নিহিত কোণ |
সমকোণ কাকে বলে
৯০° কোণকে সমকোণ বলে ।
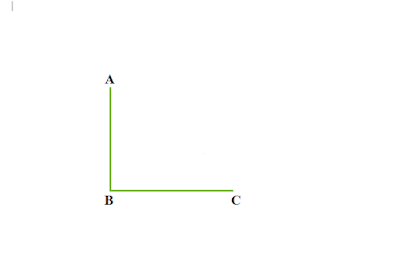 |
| চিত্র : ∠ABC একটি সমকোণ |
সরল কোণ কাকে বলে
১৮০° কোণকে সরল কোণ বলে।
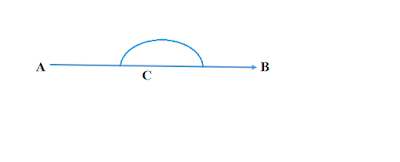 |
| চিত্র : ∠ACB একটি সরলকোণ |
সূক্ষ্মকোণ কাকে বলে
৯০° অপেক্ষা ছোট কোণকে সূক্ষ্মকোণ বলে ।
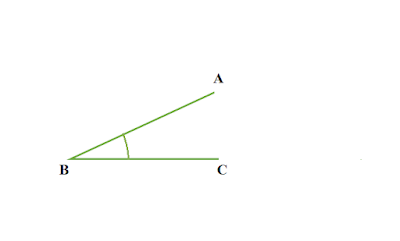 |
| চিত্র : ∠ABC একটি সূক্ষ্,মকোণ |
স্থূল কোণ কাকে বলে
৯০° অপেক্ষা বড় এবং ১৮০° অপেক্ষা ছোট কোণকে স্থূলকোণ বলে ।
 |
| চিত্র : ∠ABC একটি স্থূলকোণ |
পূরক কোণ কাকে বলে
দুইটি সন্নিহিত কোণের সমষ্টি ৯০° হলে, তাদের একটি কোণকে অপর কোণের পূরক কোণ বলে ।
 |
| চিত্র : ∠ABD এবং ∠DBC পরস্পর পূরক কোণ |
সম্পূরক কোণ কাকে বলে
দুইটি সন্নিহিত কোণের সমষ্টি ১৮০° দুইটি সন্নিহিত কোণের সমষ্টি ৯০° হলে, তাদের একটি কোণকে অপর কোণের পূরক কোণ বলে । হলে, তাদের একটি কোণকে অপর কোণের সম্পূরক কোণ বলে ।
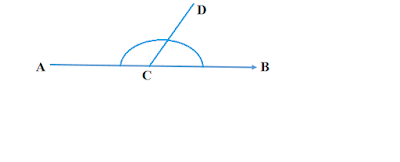 |
| চিত্র : ∠ACD এবং ∠DCB পরস্পর সম্পূরক কোণ |
বিপ্রতীপ কোণ কাকে বলে
দুইটি সরল রেখা পরস্পরকে ছেদ করলে ছেদ বিন্দুতে যে চারটি কোণ উৎপন্ন হয় তাদের বিপরীত কোণদ্বয়ের একটিকে অপরটির বিপ্রতীপ কোণ বলে ।
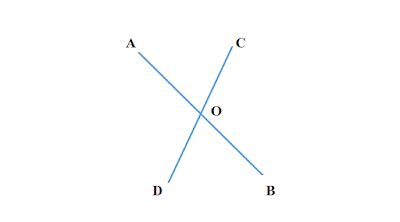 |
| চিত্র : ∠AOD এবং ∠COB পরস্পর বিপ্রতীপ কোণ । আবার ∠AOC এবং ∠DOB পরস্পর বিপ্রতীপ কোণ |
একান্তর কোণ কাকে বলে
একটি সরল রেখা একাধিক সরলরেখাকে ছেদ করলে ছেদক রেখার বিপরীত পাশে উৎপন্ন কোণগুলোকে পরস্পর একান্তর কোণ বলে ।
 |
| চিত্র : ∠AEF এবং ∠DFE পরস্পর একান্তর কোণ |
অনুরূপ কোণ কাকে বলে
একটি সরল রেখা একাধিক সরলরেখাকে ছেদ করলে ছেদক রেখার একই পাশে উৎপন্ন কোণগুলোকে পরস্পর অনুরূপ কোণ বলে ।
 |
| চিত্র : ∠AEF এবং ∠CFY পরস্পর একান্তর কোণ |
আরো পড়তে পারেন
ত্রিভুজ কাকে বলে
তিনটি সরল রেখা দ্বারা সীমাবদ্ধ ক্ষেত্রকে ত্রিভুজ বলে ।
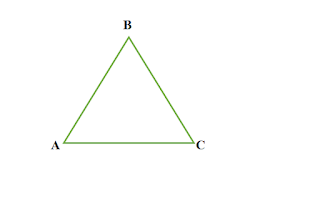 |
| চিত্র : ABC একটি ত্রিভুজ |
সমবাহু ত্রিভুজ কাকে বলে
যে ত্রিভুজের তিনটি বাহু পরস্পর সমান তাকে সমবাহু ত্রিভুজ বলে ।
 |
| চিত্র : △ABC একটি সমবাহু ত্রিভুজ |
সমদ্বিবাহু ত্রিভুজ
যে ত্রিভুজের দুইটি বাহু পরস্পর সমান তাকে সমদ্বিবাহু ত্রিভুজ বলে ।
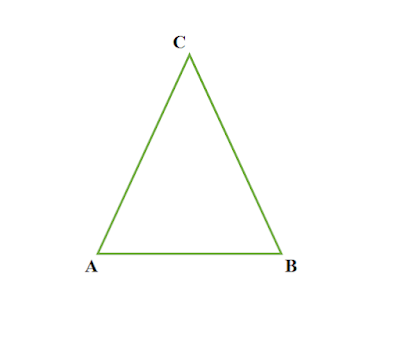 |
| চিত্র : △ABC একটি সমদ্বিবাহু ত্রিভুজ |
বিষমবাহু ত্রিভুজ কাকে বলে
যে ত্রিভুজের কোনো বাহুই পরস্পর সমান নয় তাকে বিষমবাহু ত্রিভুজ বলে ।
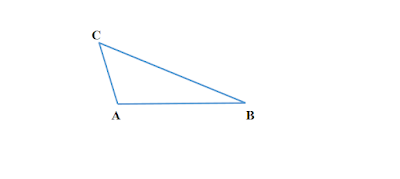 |
| চিত্র : △ABC একটি বিষমবাহু ত্রিভুজ |
সমকোণী ত্রিভুজ কাকে বলে
যে ত্রিভুজের একটি কোণ সমকোণ তাকে সমকোণী ত্রিভুজ বলে ।
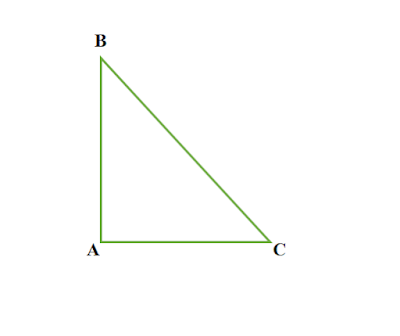 |
| চিত্র : △ABC একটি সমকোণী ত্রিভুজ |
সূক্ষ্মকোণী ত্রিভুজ কাকে বলে
যে ত্রিভুজের প্রত্যকেটি কোণই সমকোণের ছেয়ে ছোট তাকে সূক্ষ্মকোণী ত্রিভুজ বলে ।
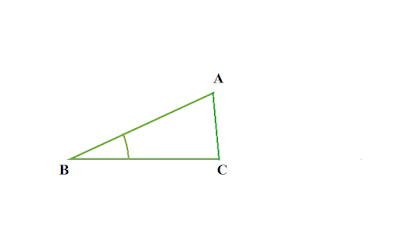 |
| চিত্র : △ABC একটি সূক্ষ্মকোণী ত্রিভুজ |
স্থুলকোণী ত্রিভুজ কাকে বলে
যে ত্রিভুজের একটি কোণ সমকোণের ছেয়ে বড় তাকে স্থুলকোণী ত্রিভুজ বলে ।
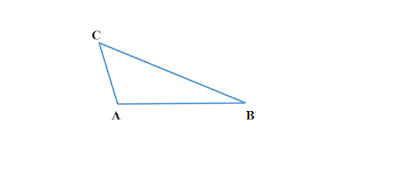 |
| চিত্র : △ABC একটি স্থূলকোণী ত্রিভুজ |
মধ্যমা কাকে বলে
ত্রিভুজের যে কোনো শীর্ষবিন্দু হতে উহার বিপরীত বাহুর মধ্যবিন্দুর সংযোজক সরলরেখাকে মধ্যমা বলে ।
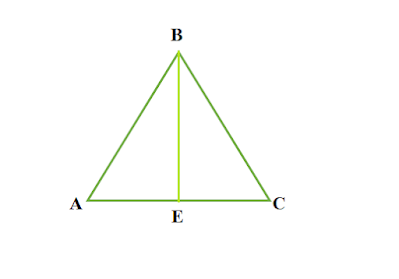 |
| চিত্র : BE, △ABC এর একটি মধ্যমা |
ভূমি কাকে বলে
সমকোণী ত্রিভুজের সমকোণ সংলগ্ন আনুভূমিক রেখাকে ভূমি বলে ।
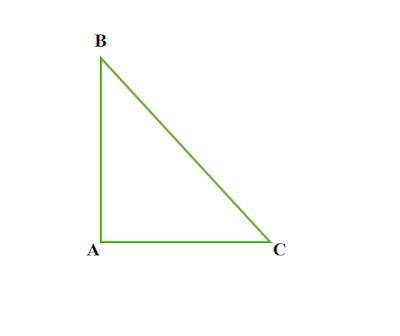 |
| চিত্র : AC, △ABC এর ভূমি |
অতিভুজ কাকে বলে
সমকোণী ত্রিভুজের সমকোণের বিপরীত বাহুকে অতিভুজ বলে ।
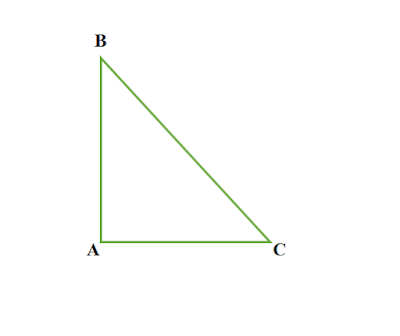 |
| চিত্র : BC, △ABC এর অতিভুজ |
চতুর্ভুজ কাকে বলে
চারটি সরল রেখা দ্বারা সীমাবদ্ধ ক্ষেত্রকে চতুর্ভুজ বলে ।
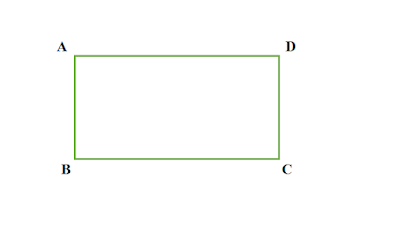 |
| চিত্র : ABCD একটি চতুর্ভুজ |
আয়ত কাকে বলে
যে চতুর্ভুজের বিপরীতবাহুগুলো পরস্পর সমান ও সমান্তরাল এবং প্রত্যেকটি কোণ সমকোণ, তাকে আয়ত বলে ।
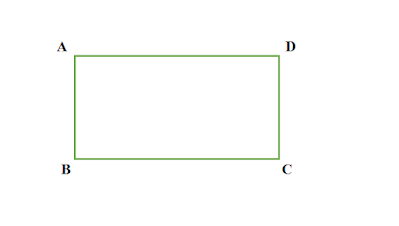 |
| চিত্র : ABCD একটি আয়ত |
সমান্তরিক কাকে বলে
যে চতুর্ভুজের বিপরীতবাহুগুলো পরস্পর সমান ও সমান্তরাল এবং কোণগুলো সমকোণ নয়, তাকে সামান্তরিক বলে ।
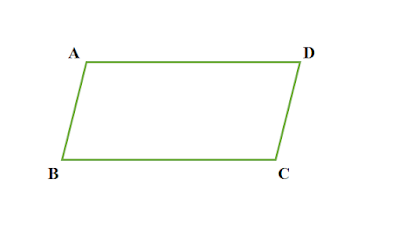 |
| চিত্র : ABCD একটি সমান্তরিক |
বর্গক্ষেত্র কাকে বলে
যে চতুর্ভুজের চারটি বাহু পরস্পর সমান ও সমান্তরাল এবং প্রত্যেকটি কোণ সমকোণ, তাকে বর্গক্ষেত্র বলে ।
 |
| চিত্র : ABCD একটি বর্গ |
রম্বস কাকে বলে
যে চতুর্ভুজের চারটিবাহু পরস্পর সমান ও সমান্তরাল এবং কোণগুলো সমকোণ নয়, তাকে রম্বস বলে ।
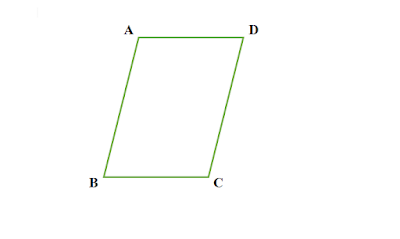 |
| চিত্র : ABCD একটি রম্বস |
ট্রাপিজিয়াম কাকে বলে
যে চতুর্ভুজের দুইটি বাহু সমান্তরাল এবং অপর দুইটি বাহু সমান্তরাল নয়, তাকে ট্রাপিজিয়াম বলে ।
 |
| চিত্র : ABCD একটি ট্রাপিজিয়াম |
কর্ণ কাকে বলে
কোন চতুর্ভুজের দুইটি বিপরীত কোণের সংযোগ সরলরেখাকে কর্ণ বলে ।
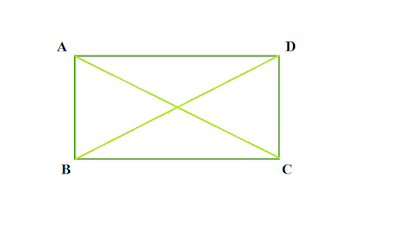 |
| চিত্র : AC এবং BD দুটি কর্ণ |
পরিসীমা কাকে বলে
কোনো সমতলিক ক্ষেত্র যতগুলো বাহু দ্বারা সীমাবদ্ধ থাকে সেই বাহুগুলোর দৈর্ঘ্যের সমষ্টিকে পরিসীমা বলে ।
 |
| চিত্র : AB+BC+CD+AD হলো ABCD চতুর্ভুজের পরিসীমা |
ক্ষেত্রফল কাকে বলে
কোনো সীমাবদ্ধ ক্ষেত্র যতটুকু স্থান দখল করে থাকে তাকে ক্ষেত্রফল বলে ।
বৃত্ত কাকে বলে
একটি নির্দিষ্ট বিন্দুকে কেন্দ্র করে সর্বদা সমান দূরত্ব বজায় রেখে একটি বক্ররেখা যদি কোনো স্থানকে আবদ্ধ করে করে তবে তাকে বৃত্ত বলে ।
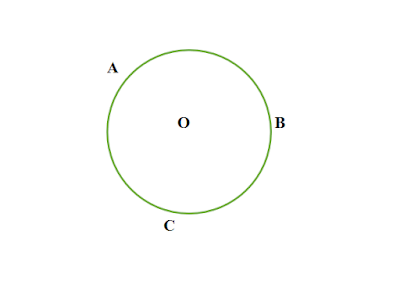 |
| চিত্র : O কেন্দ্র বিশিষ্ট ABC একটি বৃত্ত |
বৃত্তের কেন্দ্র কাকে বলে
বৃত্তের যে নির্দিষ্ট স্থির বিন্দু থেকে পরিধি সর্বদা সমান দূরে অবস্থান করে তাকে বৃত্তের কেন্দ্র বলে ।
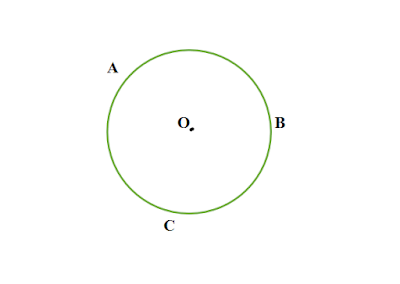 |
| চিত্র : O হলো ABC বৃত্তের কেন্দ্র |
ব্যাস কাকে বলে
বৃত্তের কেন্দ্র ভেদ করে যে সরল রেখা কেন্দ্রের উভয় পাশে পরিধি পর্যন্ত যায় তাকে ব্যাস বলে।
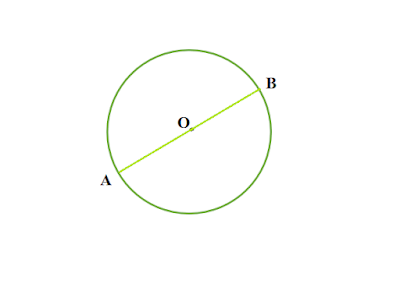 |
| চিত্র : O কেন্দ্র বিশিষ্ট বৃত্তের ব্যাস AB |
ব্যাসার্ধ কাকে বলে
কেন্দ্র থেকে পরিধি পর্যন্ত দূরত্বকে ব্যাসার্ধ বলে ।
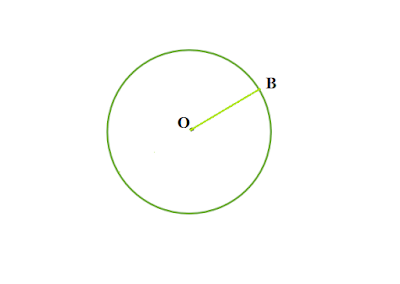 |
| চিত্র : O কেন্দ্র বিশিষ্ট বৃত্তের ব্যাসার্ধ OB |
জ্যা কাকে বলে
যে সরল রেখা বৃত্তের কেন্দ্র ভিন্ন পরিধির যে কোনো দুই বিন্দুকে সংযোগ করে তাকে জ্যা বলে।
 |
| চিত্র : O কেন্দ্র বিশিষ্ট বৃত্তের জ্যা AB |
বৃত্তের পরিধি কাকে বলে
যে বক্ররেখা দ্বারা বৃত্তটি সীমাবদ্ধ হয় তার দৈর্ঘ্যকে বৃত্তের পরিথি বলে।
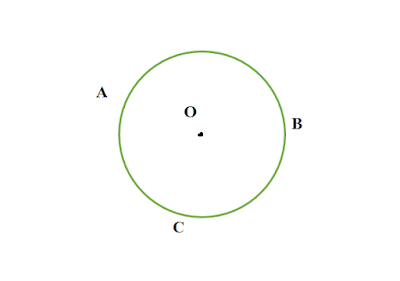 |
| চিত্র : O কেন্দ্র বিশিষ্ট বৃত্তে ABC বৃত্তের পরিধি |
বৃত্তচাপ কাকে বলে
বৃত্তের পরিধির যে কোনো অংশকে বৃত্তচাপ বলে ।
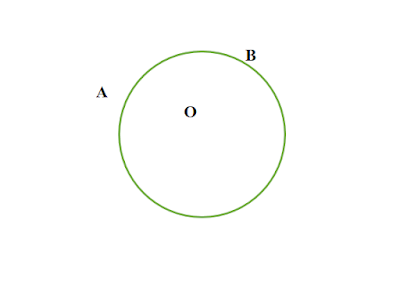 |
| চিত্র : AB রেখা বৃত্তচাপ |
অর্ধবৃত্ত কাকে বলে
বৃত্তের অর্ধেককে অর্ধবৃত্ত বলে ।
 |
| চিত্র : ABC অর্ধবৃত্ত |
বৃত্তের উপচাপ কাকে বলে
যে বৃত্তচাপ অর্ধবৃত্ত অপেক্ষা ছোট তাকে বৃত্তের উপচাপ বলে ।
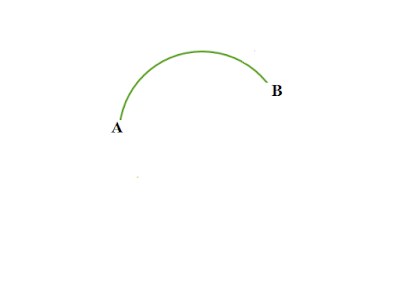 |
| চিত্র : AB বৃত্তের উপচাপ |
অধিচাপ কাকে বলে
যে চাপ অর্ধবৃত্ত অপেক্ষা বড় তাকে অধিচাপ বলে ।
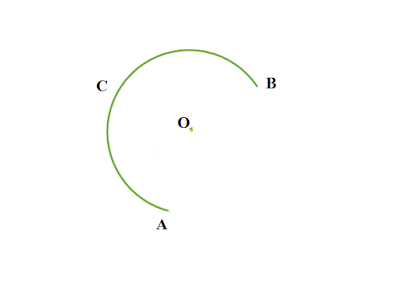 |
| চিত্র : ACB বৃত্তের অধিচাপ |
ঘনবস্তু কাকে বলে
যে বস্তুর দৈর্ঘ্য, প্রস্থ ও উচ্চতা আছে তাকে ঘনবস্তু বলে ।
 |
| চিত্র : ABCDEFGH একটি ঘনবস্তু |
তল কাকে বলে
বস্তুর পিঠ বা উপরি ভাগকে তল বলে ।
 |
| চিত্র : EFGH একটি তল |
ত্রিমাত্রিক কাকে বলে
যে বস্তুর তিনটি মাত্রা আছে তাক ত্রিমাত্রিক বলে ।
সুষম ষড়ভুজ কাকে বলে
ছয়টি বাহু দ্বারা সীমাবদ্ধ ক্ষেত্রকে ষড়ভুজ বলে । এবং যে ষড়ভুজের সবগুলো বাহু পরস্পর সমান তাকে সুষম ষড়ভুজ বলে ।
 |
| চিত্র : ABCDEF একটি সুষম ষড়ভুজ |
আশা করি জ্যামিতি শেখার উদ্যোগ নামক আজকের আর্টকেলটি তোমাদের উপকারে আসবে । ভালো লাগলে বন্ধুদের সাথে শেয়ার করে তাদেরকেও জানার সুযোগ করে দিও । এছাড়াও আরো কোনো বিষয় জানার প্রয়োজন হলে আমাদের প্রশ্ন করতে পারো । আমার চেষ্টা করো শিঘ্রই তোমাদের প্রশ্নগুলোর উত্তর প্রদান করতে ।
আরো পড়তে পারো
