জার্মান গণিতবিদ জর্জ ক্যান্টর সর্ব প্রথম সেট সম্পর্কে ধারণা প্রদান করেন । সেট সংক্রান্ত তাঁর ব্যাখ্যা গণিত শাস্ত্রে সেটতত্ত্ব ( Set Theory ) হিসেবে পরিচিত । অষ্টম শ্রেণির গণিত - এ সেট বীজগণিতের অন্তর্ভূক্ত । অষ্টম শ্রেণির গণিত বইয়ের ৭ম অধ্যায়ে শুধু মাত্র সেট সম্পর্কে শিক্ষার্থীদের কিছু ধারণা প্রদান করার চেষ্টা করা হয়েছে । তবে নবম - দশম শ্রেণির গণিত বইয়ের ২য় অধ্যায়ে সেট ও ফাংশন সম্পর্কে বিস্তারিত বর্ণনা করা হয়েছে ।
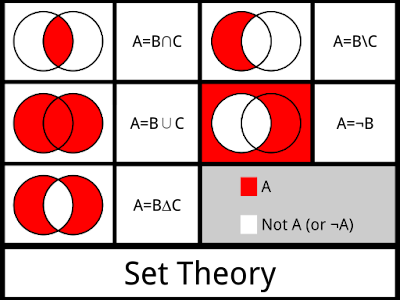 |
| সেট তত্ত্ব ছবি : commons.wikimedia.org |
আমার অষ্টম শ্রেণির গণিত ৭ম অধ্যায়ের সকল নিয়মগুলো বিচার বিশ্লেষণ করে সেট এর অংক সৃজনশীল প্রশ্ন গুলো প্রণয়ন করেছি যাতে উক্ত অধ্যায়ের সকল নিয়মগুলো এর মধ্যে অন্তর্ভূক্ত থাকে । যাতে করে পরীক্ষার্থীরা এ অধ্যায় থেকে আসা যে কোনো সৃজনশীল প্রশ্নের উত্তর প্রদান করতে সক্ষম হয় । এছাড়াও এ আর্টিকেলে সেট কাকে বলে? , সেট এর প্রকারভেদ, সেট প্রক্রিয়া, সেট গঠন প্রক্রিয়া সম্পর্কে বিস্তারিত বর্ণনা করা হয়েছে । যা জানা প্রত্যেক শিক্ষার্থীর জন্য গুরুত্বপূর্ণ ।
সেট ( Set ) কাকে বলে
বাস্তব বা চিন্ত জগতের সু - সংজ্ঞায়িত বস্তুর সমাবেশ বা সংগ্রহকে সেট ( Set ) বলে । সেটকে সাধারণত ইংরেজী বর্ণমালার বড় হাতের অক্ষর A, B, C,.... দ্বারা প্রকাশ করা হয় । যেমন : 2, 3, 4 সংখ্যার সেট A = {2, 3, 4}
সেটের প্রত্যেক বস্তু বা সদস্যকে সেটের উপাদান (Element) বলে । যেমন : A = {2, 3, 4} হলে , A সেটের উপাদান 2, 3 এবং 4 । উপাদান প্রকাশের চিহ্ন ∈ ( belongs to ) । যেমন : 2∈A একে পড়া হয় 2 belongs to A
আরো পড়তে পারেন
সেটের প্রকারভেদ
ফাঁকা সেট ( Empty set ) কাকে বলে ?
যে সেটের কোনো উপাদান নেই তাকে ফাঁকা সেট ( Empty set ) বলে । ফাঁকা সেট কে ∅ দ্বারা প্রকাশ করা হয় ।
উপসেট ( Subset ) কাকে বলে ?
কোনো সেট থেকে যতগুলো সেট গঠন করা যায় , এদের প্রত্যেককে ঐ সেটের উপসেট ( Subset ) বলে । উপসেটকে ⊆ দ্বারা প্রকাশ করা হয় ।
প্রকৃত উপসেট ( Proper Subset ) কাকে বলে ?
কোনো সেট থেকে গঠিত উপসেটের মধ্যে যে উপসেটগুলোর উপাদান সংখ্যা প্রদত্ত সেটের উপাদান সংখ্যা অপেক্ষা কম এদেরকে প্রকৃত উপসেট ( Proper Subset ) বলে । যেমন : X = {1, 2, 3, 4,} এবং Y = {2, 3} দুইটি সেট । এখানে Y এর সকল উপাদান X সেটে বিদ্যমান এবং Y সেটের উপাদান X সেটের উপাদান সংখ্যা থেকে কম । সুতরাং Y সেট X সেটের প্রকৃত উপসেট । প্রকৃত উপসেটকে ⊂ দ্বারা প্রকাশ করা হয় ।
সার্বিক সেট ( Universal ) কাকে বলে ?
সংশ্লিষ্ট সকল সেট যদি একটি নির্দিষ্ট সেটের উপসেট হয় তবে ঐ নির্দিষ্ট সেটকে তার উপসেট সাপেক্ষে সার্বিক সেট ( Universal )বলে । সার্বিক সেটকে U দ্বারা প্রকাশ করা হয় ।
পূরক সেট ( Complement of a Set ) কাকে বলে ?
যদি U সেটটি সার্বিক সেট এবং A সেটটি U সেটের উপসেট হয় তাহলে A সেটের বহির্ভূত সকল উপাদান নিয়ে গঠিত সেটকে A সেটের পূরক সেট ( Complement of a Set ) বলে । A এর পূরক সেটকে A′ বা `A^c` দ্বারা প্রকাশ করা হয় ।
সেট প্রক্রিয়া
সংযোগ সেট ( Union of sets ) কাকে বলে ?
একের অধিক সেটের উপাদান নিয়ে গঠিত সেটকে সংযোগ সেট ( Union of sets ) বলে । সংযোগ সেট ∪ দ্বারা প্রকাশ করা হয় ।
ছেদ সেট ( Intersection of Sets ) কাকে বলে ?
একাধিক সেটের সাধারণ উপাদান নিয়ে গঠিত সেটকে ছেদ সেট ( Intersection of Sets ) বলে। ছেদ সেট ∩ দ্বারা প্রকাশ করা হয় ।
নিশ্ছেদ সেট কাকে বলে
যদি দুইটি সেটের উপাদান গুলোর মধ্যে কোনো সাধারণ উপাদান না থাকে, তবে সেট দুইটিকে পরস্পর নিশ্ছেদ সেট বলে ।
শক্তি সেট (Power Sets ) কাকে বলে ?
কোনো সেটের সকল উপসেট দ্বারা গঠিত সেটকে ঐ সেটের শক্তি সেট (Power Sets ) বলে । যেমন : A সেটের শক্তি সেটকে P(A) দ্বারা প্রকাশ করা হয় ।
ভেনচিত্র কাকে বলে
জন ভেন ( ১৮৩৪ - ১৮৮৩ ) চিত্রের সাহায্যে সেট প্রকাশ করার পদ্ধতি প্রবর্তন করেন । এই চিত্রগুলো তার নামানুসারে ভেন চিত্র নামে পরিচিত । ভেনচিত্রে সাধারণত আয়তাকার ও বৃত্তাকার ক্ষেত্র ব্যবহার করা হয় ।
সেট প্রকাশের পদ্ধতি কয়টি
প্রধানত সেট দুই পদ্ধতিতে প্রকাশ করা হয় । যথা :
১. তালিকা পদ্ধতি ( Tabular Method )
২. সেট গঠন পদ্ধতি ( Set Builder Method )
তালিকা পদ্ধতি ( Tabular Method ) : যে পদ্ধতিতে সেটের সকল উপাদান সুনির্দিষ্ট ভাবে উল্লেখ করে দ্বিতীয় বন্ধনী { } এর মধ্যে আবদ্ধ করা হয় এবং একাধিক উপাদান থাকলে 'কমা' ( , ) ব্যবহার করে উপাদানগুলোকে পৃথক করা হয় তাকে তালিকা পদ্ধতি ( Tabular Method ) বলে । যেমন : A = { 1, 2,3 }
সেট গঠন পদ্ধতি ( Set Builder Method ) : যে পদ্ধতিতে সেটের সকল উপাদান সুনির্দিষ্ট ভাবে উল্লেখ না করে উপাদান নির্ধারণে জন্য শর্ত দেওয়া থাকে তাকে সেট গঠন পদ্ধতি ( Set Builder Method ) বলে । যেমন : { x : x স্বাভাবিক সংখ্যা, x<10 }
শর্ত হিসেবে স্বাভাবিক সংখ্যা, স্বাভাবিক জোড় সংখ্যা, স্বাভাবিক বিজোড় সংখ্যা, গুণনীয়ক সংখ্যা, গুণিতক সংখ্যা, মৌলিক সংখ্যা, পূর্ণ সংখ্যা ইত্যাদি দেওয়া থাকে ।
অষ্টম শ্রেণির সেট এর অংক সৃজনশীল প্রশ্ন
১. কোনো পরীক্ষায় 80% গণিতে এবং 70% বাংলায় পাস করলো । উভয় বিষয়ে পাস করলো 60%
ক. তথ্যাবলি ভেনচিত্রের মাধ্যমে প্রকাশ কর ।
খ. উভয় বিষয়ে শতকরা কত জন ফেল করেছে ?
গ. উভয় বিষযে 15% ফেল করলে উভয় বিষয়ে শতকরা কতজন পাস করেছে ?
২.
ক. U সেটকে তালিকা পদ্ধতিতে প্রকাশ কর ।খ. প্রমাণ কর যে, (PUQ)∩(PUR) = PU(Q∩R)
গ. দেখাও যে, (P∩R)' = P'∩R'
আরো পড়তে পারেন
৩. `U=\{4<x\leq10\}`
P = { x : x বিজোড় সংখ্যা এবং 4<x<10 }
`Q=\{x:7<2x\leq18\}`
ক. U তালিকা পদ্ধতি নির্ণয় কর ।
খ. PUQ ও P∩Q নির্ণয় কর এবং সেট গঠন পদ্ধতিতে প্রকাশ কর ।
গ. R = Q' এবং S = P' হলে R - S নির্ণয় কর ।
৪. A = { 3, 6, 9, 12, 15, 18 }
B = { x : x, 24 এর গুণনীয়ক }
ক. A সেটকে সেট গঠন পদ্ধতিতে প্রকাশ কর ।
খ. A ও B এর পূরক সেট নির্ণয় আরে ভেনচিত্র আঁক । A ও B এর সার্বিক সেট থেকে উপসেট নির্ণয় কর ।
গ. প্রমাণ কর যে, (AUB)' = A'UB'
৫. কোনো ছাত্রাবাসে 65% ছাত্র মাছ পছন্দ করে, 55% ছাত্র মাংস পছন্দ করে এবং 40% ছাত্র উভয়টি পছন্দ করে ।
ক. সংক্ষিপ্ত পদ্ধতিতে বিবরণসহ তথ্যগুলো ভেনচিত্রে প্রকাশ কর ।
খ. উভয় খাদ্য শতকরা কত জন ছাত্র পছন্দ করে তা নির্ণয় কর ।
গ. যারা শুধু একটি খাদ্য পছন্দ করে তাদের সংখ্যার গুণনীয়ক সেটের ছেদ সেট নির্ণয় করা ?
৬. যে সকল স্বাভাবিক সংখ্যা দ্বারা 346 ও 556 কে ভাগ করলে প্রতি ক্ষেত্রে 31 অবশিষ্ট থাকে । তাদের সেট যথাক্রমে A ও B
ক. A সেট কে তালিকা পদ্ধতিতে প্রকাশ কর ।
খ. A∩B নির্ণয় কর ।
গ. A∩B ভেনচিত্র দেখাও এবং A∩B এর উপসেটগুলো নির্ণয় কর ।
৭. সার্বিক সেট U = { 1, 2, 3, 4, 5, 6, 7 }
A = { x ∈ N : x< 7 এবং x বিজোড় সংখ্যা }
B = { x ∈ N : x< 7 এবং x জোড় সংখ্যা }
C = { x ∈ N : x< 4 এবং x মৌলিক সংখ্যা }
ক. A ও B সেটকে তালিকা পদ্ধতিতে প্রকাশ কর ।
খ. (AUB)∩(AUC) নির্ণয় কর ।
গ. (BUC)' এর উপসেট নির্ণয় কর ।
অফলাইনে অনুশীলনের জন্য নিচ থেকে অষ্টম শ্রেণির সেট এর অংক সৃজনশীল প্রশ্ন গুলোর ছবি ডাউনলোড করে নিতে পারো ।
আশা করি সেট এর অংক সৃজনশীল তোমাদের উপকারে আসবে । ভালো লাগলে বন্ধুদের সাথে শেয়ার করে তাদেরকেও জানার সুযোগ করে দিও । এছাড়াও আরো কোনো বিষয় জানার প্রয়োজন হলে আমাদের প্রশ্ন করতে পারো । আমার চেষ্টা করো শিঘ্রই তোমাদের প্রশ্নগুলোর উত্তর প্রদান করতে ।
আরো পড়তে পারো







